Stata ignores interference factors, endogeneity, and estimates of missing variable biases
initial thoughts
Since causality is elusive, assessing the causal relationship of data is one of the researcher's efforts. Before ignoring the interference factor, endogeneity, missing variable or a wrong model, the estimation of the predicted value and the interest effect will be inconsistent, and the causal relationship will become more blurred.
Testing for causality is an alternative. However, conducting control experiments may not be feasible. For example, policy makers cannot levy taxes on a random basis. In the absence of experimental data, an alternative is to use tool variables or control function methods.
Stata has many built-in estimates to implement these potential workarounds and tools, as well as an assessment tool to make it impossible to cover the built-in evaluation tools. The following two examples illustrate the two possibilities of linear models. In the following articles, we discuss nonlinear models.
Linear model case
Let's start with a linear model of two covariates, x1 and x2. In this model, x1 is independent of the error term? This is the given condition E(x1?)=0, x1 is an exogenous variable, and x2 is an error-related term; the given condition is E(X2?)≠0, x2 Is an endogenous variable. The model is as follows:
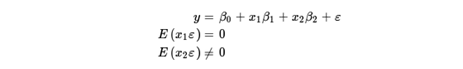
In fact, X2 is related to unobservable factors, which means that linear regression fitting models are used to obtain inconsistent parameter estimates. One option is to use a two-stage least squares estimation. The two-stage least squares method is effective, and it is necessary to specify a correct model for x2 including a variable z1, which is independent of the unobservable variable X1 of the benefit result. We also need that z1 and x1 are independent of unobservable results, and that the x2 equation is also unobservable. The expression is as follows:
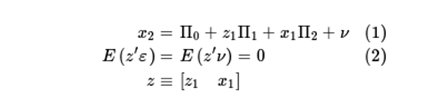
In the relationship of (1), it is suggested that x2 can be divided into two parts, one is related to ?, the crux of the problem is V, and the other is irrelevant.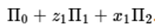 
. The key to the two-stage least squares method is to obtain an estimate that is consistent with the latter part of x2.
The following is a simulation of data that satisfies the above assumptions:
If the model parameters are estimated by least squares, you will get
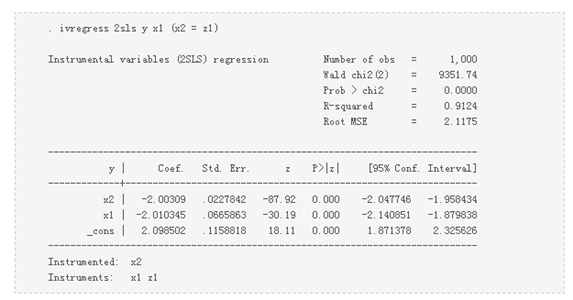
Restore the coefficient values ​​of the covariates, x1 is -2, x2 is -2, and 2 is a constant.
Model parameters can also be recovered using the sem structural equation model. The key here is to specify two linear equations and declare that the unobservable parts of the two equations are related. Interestingly, the model is not satisfied with the sem estimate of the unobservable hypothesis joint normality, so a consistent estimate is obtained, as shown by the coefficient values ​​for equation y in the output table below:
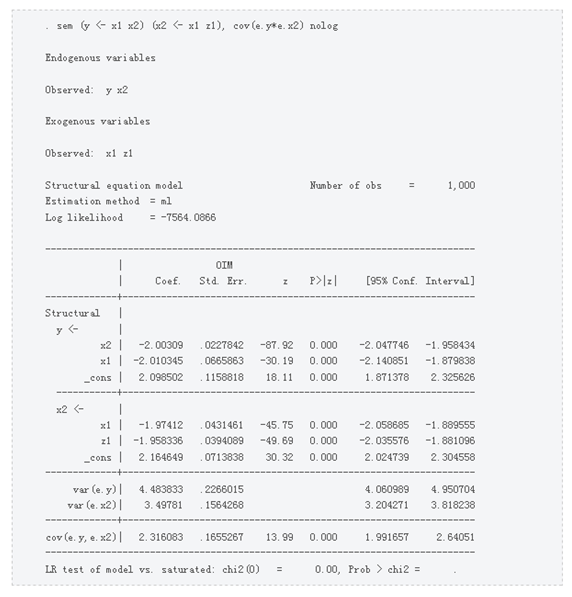
The sem syntax requires writing two linear equations. Use a <- to establish an inner variable and declare two inner variables as unobservable variables, represented by the associated ey and e.x2. Use the option cov(ey*e.x2) to specify the correlation.
The coefficients and standard errors obtained using sem are exactly the same as those obtained by the least squares method. This equation occurs in the moment estimation, like two-stage least squares and generalized moment estimation (GMM), or when the moment condition and the fractional equation are the same, based on the likelihood estimation. Therefore, even if the assumptions are different, the estimated equations are the same. The estimation equations for these models are provided by (2).
You can also fit this model using gmm in gmm. Methods as below:
1: Write the residual of the endogenous variable equation. Examples are as follows:
2: Use all exogenous variables as tools in the system, in this case x1 and z1.
Use gmm to get the following:
Again, use ivregress and gsem. to get the same parameter values, but the standard error is different. The reason is that the gmm calculation robust standard error is the default. If you calculate ivregress with a robust standard error, the result is exactly the same:
Another method is to use the control function method to get the parameters of interest. Use the regression residuals of the endogenous variable x2 from tools x1 and z1,
As a regression factor y for x1 and x2. The way to use gmm to implement control functions is as follows:
As shown in the previous example, defining the residuals and tools, gmm uses these two pieces of information to create moment conditions. In the above example, the regression residuals of the endogenous variables of the model exogenous variables are also residuals and tools. Therefore, I did not regard them as exogenous tools. Instead, in the endogenous variable regression of eq3, a moment condition is manually established for the residual.
In the first three examples, the same result is again given using the control function method. The first example uses the estimates already in Stata. In the latter two examples, the estimation tool was used to obtain large model estimates.
Conclusion
Estimating existing endogenous model parameters and related problems is quite difficult. The above example illustrates how commands can be used to estimate the parameters of these models in Stata. The purpose is also to show how to evaluate these models using gmm and sem.
It developed by a professional team of Queshan handmade violin makers after decades of development and debugging. Produced by Haoya Musical Instrument Co., LTD, the materials are made of imported steel core and Aluminum-magnesium alloy, using advanced winding production technology, suitable for all new Violins.
Keywords:Violin Strings Full Size.Factory Custom Strings Full Size
Features:
1. Imported materials and wire wrapping technology;
2. The G string is thicker than ordinary strings;
3. The four strings have average sound quality, wide range and great tension;
4. No rust, no stripping, long service life;
5. One more spare E string.
6.Excellent pitch performance,bright and clear,fast response
Professional Violin Steel Strings,New Violins String,Violin Steel Strings,Custom Strings Full Size
Queshan Wahyo Violin Ltd , https://www.wahyoviolin.com